homepage
coding shit
some of my methods for solving some project euler problems i found interesting/challenging.
spoilers ahead if you want to try for yourself do not look at solutions.
it is very unlikely these are optimals solutions.
listed: 31, 78, 173, 174, 109, 144, 86, 102, 204, 351
#31 - Coin Sums
how many ways can you make $2 using the following coins: {1c, 2c, 5c, 10c, 20c, 50c, $1, $2}?
initial thoughts, i'll define p(n) to be the number of ways you can reach n using the set of coins.
this means p(0) = p(1) = 1. the goal is to find p(200).
p(n) must be a non-decreasing function because you can attach 1c to every solution for the previous n.
so p(n) >= p(n-1). can i repeat this process for the other coins. so for applying the same logic as the 1c we know p(n) >= p(n-2).
so if i account for all coins like this we get p(n) = Σ꜀ p(n-c), for c in coins.
unfortunately this double counts many solutions i.e. one solution to p(4) is (2, 1, 1) and a solution to p(5) is (2, 2, 1)
the method described above would get (2, 1, 1, 2) as a solution to p(6) twice. (2, 1, 1) + (2) and (2, 2, 1) + (1)
to stop double counting, make sure the coins picked in descending order. so if a coin c is picked, then no coin greater then c can be picked until the target is reached.
this ensures that all solutions which reach the target are unique. and therefore a simple recursive solution is applicable.
since target and coin set were not very big i didnt bother trying to optimise anymore. i know this is a slow solution, lots of redundant calculations. better solution applied to next problem.
pe difficulty: 5/100
show solution
solved: 26/10/25
#78 - Coin Partitions
the partition function p(n) describes how many unique ways you can separate a number n into different piles. p(5) = 7 you solve these pretty quickly with pen and paper.
it becomes not so trivial quite fast, p(100) = 190,569,292*. the goal of this problem is to find the smallest n such that p(n) mod 1e6 = 0.
*turns out this is its own pe problem(#76 - Counting Summations), my dynamic sol gets this correct very quickly.
this problem is similar to #31 - coins sums, except we we are not limited to only groups of 1, 2, 5, 10, etc. and we do not know what our final value of n will be.
so i started by adjusting the code from my solution of that problem to account for any pile size. this worked, however is very slow due to the recalculating the same thing many times.
if i had only optimised my code at the time this problem would have been free.
okay a while later. problem not free. i thought i got a decent dynamic solution (
dynamic attempt
), always gives same answer as recursive (up to n=50).
so i modify it to run in a while loop like fashion, it gives an answer of 2301. pe says "X wrong". wtf? recheck to bigger numbers with recursive, still looks good.
in my confusion i go to google, all answers i see are refering to euler's pentagonal numbers and recurrence relations, nothing like my dynamic programming solution.
also i found what the real answer was. spoiler: not 2301, like 30x bigger. well i try my dp solution upto 60k, and its slow, too slow. O(n2) is not enough.
as for why i was getting 2301, im not sure. hopefully if i can solve with this other method, i can compare and see what went wrong.
i figured i could use similar logic to # 31, which maybe you can, but just too slow even with dynamic sol :(. so i am now going to try the method i read about online.
i think a lot of the difficulty if this problem is researching, once you find
Euler's pentagonal number thereom it is not too hard to apply
this was a bit :/ for me, cos i didnt realise there would be problems in this list that require niche mathematical theorems to solve.
so this is my implementation. i cant say i understand why this recurrence works or what pentagonal numbers have to do with it, but it works and takes like 10 seconds.
after doing this i went back and compared to my dynamic solution, turns out the dynamic sol is the same until n=300 where the solutions are 4 apart. from there they quickly diverge even further apart.
why this is i have no idea, i am curious tho.
pe difficulty: 30/100
show solution
solved: 28/10/25
#173 - Hollow Square Laminae I
how many hollow squares (see image below) can you construct using up to a million blocks?
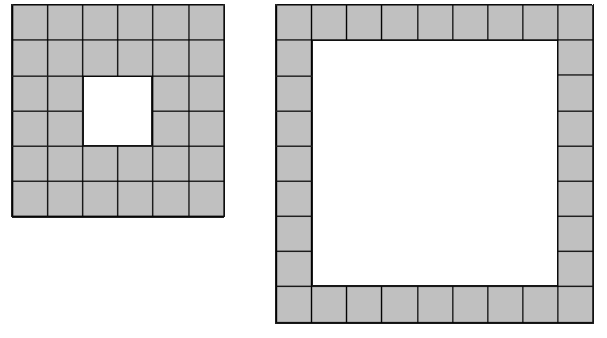
my first step was to draw a few little hollow squares to look for patterns.
initially i was thinking that i would have to account for two cases, when the "centre" of the square was 1x1 (odd) vs 2x2 (even).
i then thought of the hollow squares as a binary sequence, eg. the left square above would be 011. and tried to figure out a formula to count the number of cells from the binary sequence.
idk why this was my first approach as it would have been massively slower, huge overkill and really complicated.
luckily i noticed the number of cells in the hollow square was easily calculatable if you know the side length of the "inner" and "outer" square.
num_cells = outerN2 - innerN2
now all i needed to do was define an iterative process which checks all outer and inner N's until num_cells exceeded 1 million.
the first thing i thought of was iterating thru "edge thickness" and outerN in a nested while loop. this way innerN = outerN - edgeThickness at each step.
i found this problem easier then expected and i think this is a pretty efficient method.
pe difficulty: 30/100
show solution
solved: 26/10/25
#174 - Hollow Square Laminae II
this one just expanded on the last problem. its a bit of word salad:
If t represents the number of tiles used, we shall say t=8 is type L(1) and t=32 is type L(2). the type describes how many unique hollow squares you can construct for a given t.
Now let N(n) be the number of t ≤ 1e6 such that t is type L(n). What is Σn N(n) for n = 1-10?
so thats a lot of words but what N(n) is asking is: how many numbers under 1 million can you construct n unique hollow squares with?
using the code from the previous problem this is rather trivial. all i did was create an array which will store how many unique hollow squares each t can create.
because of the way the algorithm works in the previous problem it is guaranteed to generate all hollow squares using less then 1 mil cells without duplicates.
once the array is generated i just wrote a small function to count how many elements in the array equal some target value.
then sum that from 1 - 10. dont be like me i spent like 10 minutes getting it wrong because i was looping from 0 - 10 instead :(
pe difficulty: 40/100
show solution
solved: 26/10/25
#109 - Darts
how many unique checkouts are there in a game of darts, starting from 100 or less?
a checkout in darts must end with a double pointer and can use no more then 3 darts.
the thing that makes this problem hard is how unique is defined. so D2 S1 D1 != D1 S1 D2 because while made up of the same components they ended on different triples.
on the other hand D2 D2 D1 != D2 D1 D2 == D1 D2 D2 and S1 S3 D1 == S3 S1 D1
my idea was simple, loop thru the possible 1, 2 and 3 dart checkouts, check if they sum to n, check if they end on a double, check if has been seen before.
the check if been seen before was the tricky part because of the strict uniqueness rules of the problem.
after a bit of fucking about i created an Area(value, mult) class which each describe a unique area of the dartboard. I put all of these into an array and sorted based on points value.
then when iterating thru the possible 2 and 3 dart checkouts, i did one of those progressive nested for loops (idk if they have a proper name)
this means the combos produced in the nested for loops are guaranteed to be unique. in my experience, this technique can best be applied with nested loops over the same sorted set.
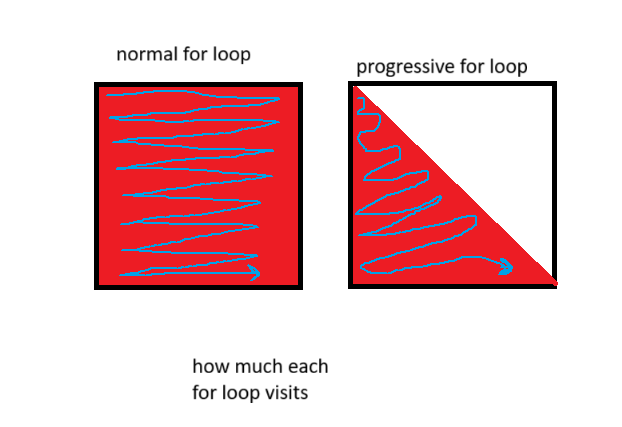

as the number of nested for loops increases it saves more time compared to the regular method. i think 2d-1 times better where d is the depth of nested for loops.
then i counted how many unique double areas that checkout had, this was the best way i could find to account for the strange uniqueness check. if it only had 1 unique double then i just continued.
if there were 2 double present in the checkout then there was one other solution, as depicted in the image above, so i added 2.
so in the right image above, the left yellow dot indicates a new found solution, say D2 D4. the other ? yellow dot represents the checkout D4 D2.
checking the uniqueness criteria we see these 2 are different, so we add 2 to the tally. if the checkout was S8 D2, we would only add 1, D2 S8 does not count.
if there were 3 unique doubles, then there were 2 other solutions. you may, like me, initially think this is meant to be 6 (3!), but remember only the last dart matters so we only add 3.
because only the total number of combinations was needed not the combinations themselves i neglected to create some sort of list of checkouts and just kept a running tally.
this was more difficult then it seemed on the tin. the difficultly mainly comes from working around the rules for what is and is not a unique checkout.
fortunately a dartboard only has 62 areas cos my algorithm is O(a3) where a is the number of areas on a dartboard.
i think my solution is decent (less then a second on my laptop :o) but would be interesting to see what the best way to solve if problem was larger; more darts, more areas, etc.
dunno why i went full on explaining mode for this paragraph, haha, even drew pictures.
pe difficulty: 45/100
show solution
solved: 27/10/25
#144 - Laser Beam Reflections
given the ellipse 4x2 + y2 = 100, a laser placed at (0, 10.1) shines a beam on the point (1.4, -9.6). the beam then reflects around the ellipse using the standard laws of reflection.
there is an opening in the ellipse between -0.01 < x < 0.01 on the y>0 side of the ellipse, where the beam can exit the ellipse. how many reflections does it take before it leaves the ellipse?
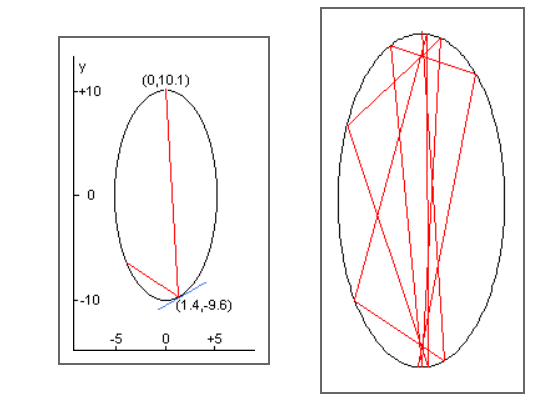
to solve this problem required to follow a small set of instructions until the exit is found:
1. find slope of line of the laser (effectively given for the first, easily solveable for all subsequent)
2. find point at which it intersects ellipse (there will be 2 solutions but the beam will have started at one of them so pick the other)
3. find the tangent slope at that point (given by -4x/y for this ellipse, given in the problem)
4. find normal to tangent at that point (-1/m, where m is slope of tangent line)
5. find slope of next line from the information gathered in last 4 steps
6. repeat steps 1-5 until new intersection with ellipse is between -0.01 < x < 0.01 and y > 0
initially i tried to algebra out everything myself, but i got stuck on step 5. luckily
this stackexchange post provided a neat solution for the new line, in terms which i had already calculated.
from there it was just looping through until the solution was found.
pe difficulty: 50/100
show solution
solved: 5/11/25
#86 - Cuboid Route
A spider is in a box with integer side lengths i,j,k. Starting in a corner it travels to the opposite corner on the shortest path.
given a box with a maximum side length M, call f(M) the number of boxes whose shortest path is an integer. find the smalled value of M s.t. f(M) is > 1,000,000.
my first thoughts were how to solve the shortest path. if you "unravel" a rectangular prism to its net.
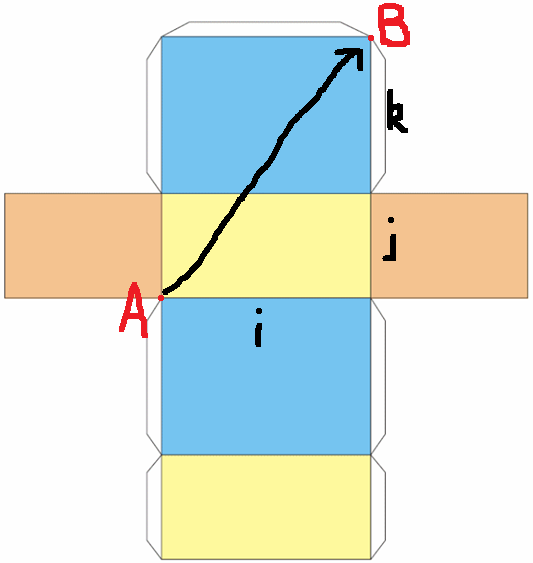
the shortest distance (s) between opposite corners (A --> B) can be solved using pytagorus thereom: s2 = i2 + (j+k)2.
so i quickly reached this point and created a brute force algorithm which worked correctly. this was too slow tho because it recalced all solutions for all m < M every time M increased.
i fugured shifting this solution to a dynamic one would be very simple. but like 40 min later i was still struggling and was getting annoyed.
so i wrote a binary search algorithm to accompany the brute force solution to create my hack solution. this works but still not that fast (even with njit) and im not satisfied by it.
if i remember/can be bothered i will return and make this an elegant solution.
pe difficulty: 35/100
show hack solution
solved: 6/11/25
#102 - Triangle Containment
you are given a list of 1000 triangles described using there vertices. return how many of them contain the origin.
so the first thing i did was construct 3 vectors from each vertice to the origin. initially i thought of summing them and then somehow using that resulting vector to do something.
i could not figure out where this strategy was going, but i realised that the angles between these vectors will sum to 360 degrees (2pi rad) iff the origin is inside the triangle.
from there it was simple, just calculate the vectors, apply cosine rule to each pair of vectors, sum the 3 resultant angles, check if equal to 2 pi.
just remember to account for floating point errors by rounding the sum of angles and 2 pi in the comparison.
this one was pretty easy and didnt take long, but i am quite satisfied with my solution. :)
pe difficulty: 15/100
show solution
*ofc this solution is only guaranteed to work for triangles because they cannot be concave polygons. this is not always true for n-gons with n > 3.
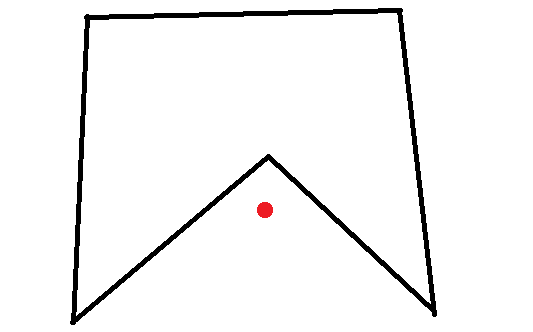
after some research it appears there are algorithms which can always guarantee the solution regardless of n, if its convex or concave or even if it has holes in it.
maybe there will be another pe problem which extends on this one.
solved: 6/11/25
#204 - Generalised Hamming Numbers
A type-n hamming number is a positive integer that has no prime factor greater then n. For examples, there are 1105 type-5 hamming numbers less then 108.
How many type-100 hamming numbers are there less then 109?
my first instinct is to generate the prime up to 100, loop through all combinations of factors and count how many are less then the target.
this brute force approach works, but too slowly. To optimise i created an array of exponents to loop through the combinations and when a given combo exceeded the target, I skipped as much as possible.
for example, with the type-5 hamming numbers exceding 1000. i have an array called primes = [2,3,5] and an array called exps=[0,0,0].
firstly i calculate my power-product, res = primes[0]exps[0] x primes[1]exps[1] x primes[2]exps[2] (ofc account for zero case :/)
i then increment this array each loop as if it was a number with different bases??? idk bout the math of this but its how my code works.
so in this example, exps[0] cannot exceed 10 (210>1000), exps[1] cannot exceed 7 (37>1000), etc.
finally there will be situation going to the next state will still exceed the target. eg. exps = [5,5,1], rule above dictates next exps = [6,5,1], but since [5,5,1] also exceeds the target, [6,5,1] is guaranteed to also.
so in this cases i skip ahead to the next state which is less then the target. this is done by setting more and more values to zero from left to right. so check if [0,6,1] exceeds, if so skip to [0,0,2].
and yea im pre happy, code ran in less then a second once numba sorted all its shit out :)
pe difficulty: 30/100
show solution
solved: 2/12/25
some more thinking on this, could you make this better by starting at the target and dividing through by decreasing primes, similar to the process in coin sums? i think this would work and allow for a dynamic progrmaming solution.
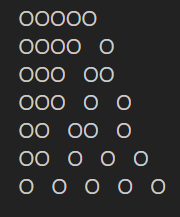
#351 Hexagonal Orchards
susppose you have an orchard where trees are placed in a hexagonal lattice. an order(n) orchard has n hexagons of increasing size, order(5) is pictured left below.
if you were standing at the centre certain trees would be blocked from view by other trees, indicated as green.
call f(n) the number of hidden trees in an order(n) orchard. solve f(108).

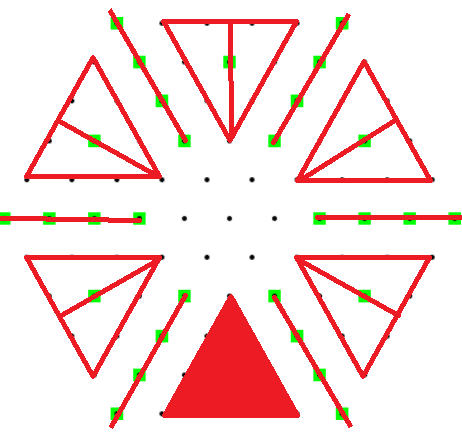
the triangle has lots of symmetry we can take advantage of. so my initial brute force solution was to run through a subtriangle row by row, check if the i, j are coprime and yada-yada.
too slow, the important step in that process is the coprime checking.
after doing some of these problems, ive learnt a bit of research can do wonders. i found the euler totient function φ(n), which is the number of integers less then n which are coprime to n.
this removes the inner loop from the brute force method, and replaces it with the totient function which is better.
the other big speed up was to count the "blocker" trees rather then hidden ones. for every blocker there is a unique set of hidden trees, which form a simple linear sequence (in terms of distance, (i, j), whatever). this sequence will be n//i long.
of course this includes the blocker tree so remove one from that. and done, number hidden trees in a subtriangle is sum of φ(i) * (n//i - 1) for i 2..n//2 + 1
only need to iterate to n//2 because any blocker tree after that, the first hidden tree will be at a row m > n, so redundant.
this code took like 15 minutes to run on my laptop, i read this pdf they give after solving and there are sub linear algorithms to solve this, which is cool, i will recreate one to use in the future. i hope they have more of these pdfs.
pe difficulty: 25/100
show solution
solved: 7/12/25
interestingly looking at f(n) for n = 10i, the solutions seem to be converging.
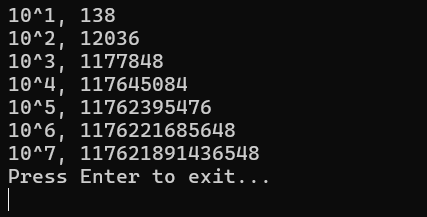
dunno what this means but is interesting. is it just kx+c where x is the totient function, i suspect so but im tired. im sure someone has done extensive research into this.
on second thought, this is just the euler totient sum function multiplied by 6. so i think the euler totient sum must approach some constant like thing.
im struggling to think of a good word for it, its like a ratio approximation for pi or the golden ratio improving as n grows, but on the right side of the decimal point.









